Question

A day-care center has a merry-go-round that consists of a uniform 240-kg circular wooden platform 4.00m in diameter. Four children run alongside the merry-go-round and push tangentially along the platform’s circumference until, starting from rest, the merry-go-round is spinning at a rate of 2.14 rev/minute. During the spin-up:

a) If each child exerts a sustained force of 26N, how far does each child run?
b) What is the angular acceleration of the merry-go-round?
SHOW ALL WORK AND STEPS PLEASE.

Answer 1

a) The distance each child ran is approximately 0.232 m

b) The angular acceleration is 0.21
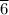`\overline 6` rad/s²

Step-by-step explanation:

The given parameters of the merry-go-round are;

The mass of the merry-go-round, m = 240-kg

The diameter of the merry-go-round, d = 4.00 m

The number of children pushing tangentially on the merry-go round = Four children

The spinning rate of the merry-go-round, n = 2.14 rev/minute

a) Given that the force exerted by each child = 26 N, we have;

The total force applied by the four children, F = 26 N × 4 = 104 N

The tangential acceleration,
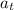`a_t` = F/m = 104 N/240-kg = 0.4
`\overline 3` m/s²

The angular acceleration, α =
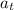`a_t`/r

Where, the radius of the merry-go-round, r = d/2

∴ r = 4.00 m/2 = 2.00 m

α = 0.4
`\overline 3` m/s²/(2.00 m) = 0.21
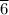`\overline 6` rad/s²

We have;

ω² = ω₀² + 2·α·Δθ

The merry-go-round starts from rest, therefore; ω₀ = 0 rad/s

ω² = 2·α·Δθ

Δθ = ω²/(2·α)

n = 2.14 rev/minute

∴ ω = 2·π×2.14/60 rad/s ≈ 0.22410 rad/s

∴ Δθ = (0.22410 rad/s)²/(2 × 0.21
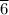`\overline 6` rad/s²) ≈ 0.11589 rad

Therefore, the angle each child ran, θ = 0.11589 rad

The distance each child ran = r·θ

∴ The distance each child ran = 2.00 m × 0.11589 rad ≈ 0.232 m

b) From part 'a' above, the tangential acceleration,
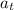`a_t` = 0.4
`\overline 3` m/s²

Angular acceleration, α =
`a_t`/r

∴ α = 0.4
`\overline 3` m/s²/(2.00 m) = 0.21
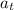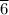`\overline 6` rad/s²

The angular acceleration = 0.21
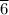`\overline 6` rad/s²