Answer:
Area of the shaded region is 223.72 square units.
Explanation:
Area of the shaded region = Area of parallelogram - Area of triangle
Area of the parallelogram = base x height
= 23.8 x 15
= 357 square feet
Area of triangle =
 x base x height
x base x height
Let the height of the triangle be represented by h, applying the Pythagoras theorem;
 =
=
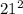 +
+
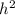
566.44 = 441 +
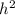
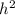 = 125.44
= 125.44
h =
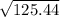
= 11.2
h = 11.2
Area of the triangle =
 x 23.8 x 11.2
x 23.8 x 11.2
= 133.28
Area of shaded region = 357 - 133.28
= 223.72
Area of the shaded region is 223.72 square units.