Question

You own a fixed income portfolio with a single 10-period zero-coupon bond with a face value of $100 million and a current yield of 6% per period. During the past 100 trading days there were 50 days when the yield on these bonds did not change, 15 days when the yield increased 1 basis point, 15 days when the yield decreased by 1 basis point, 9 days when the yield increased by 5 basis points, 9 days when the yield decreased by 5 basis points, 1 day when the yield increased by 10 basis points, 1 day when the yield decreased by 10 basis points. During this 100 day estimation period, the estimated standard deviation of daily interest rate changes equals 2.36 basis points.

1. What is 1-day 99% VAR using historical simulation?
2. What is 1-day 95% VAR using historical simulation?
3. What is the 99% 1-day Delta-Normal VAR?

Answer 1

Historical simulations Var

The lowest return shows the
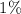`$1 \%$` of lower tail of the 'distribution' of
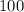`$100$` historical returns. The lowest return is (-0.0010) is the
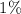`$1 \%$` of daily VAR that we would conclude that there is
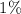`$1 \%$` of chance of the daily loss exceeding
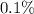`$0.1 \%$` or
`$ \$ 1$`.

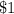Delta Normal VAR

To locate the value of
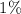`$1 \%$` VAR, we can use cumulative z-table. In this table we can look for the significance level of the VAR.

Suppose for example, if we want a
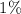`$1 \%$` VAR, we look in the table that is closest to (1 significant level) or the 1 - 0.01 = 0.9900. We can find 0.9901 and it lies at the intersection of 2.3 in left margin and also 0.03 in column heading.

Now adding the z-value in left hand margin, and the z-value at top of column where 0.9901 lies. So we get 2.3 +0.03 = 2.33, and the z-value coinciding with 99% VAR is of 2.33

`$VAR = [\hat R_P-(z)(\sigma)]V_P$`

Here,
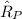`$\hat R_P$` is the expected 1 day return on portfolio

`$=[50 * 0+15* 0.0001+15* (-0.0001)+9 * 0.005+9 * (-0.0005)+1 * 0.00010+1 * (-0.0010)]/100$`= 0%

VP =
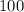`$100$` (value of portfolio)

z =
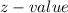`$ z- value $` corresponding with desired level of significance =
`$2.33$`

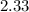
σ = standard deviation of 1 day return = 0.000246

`$VAR :[0-2.33 * 0.000246] * 100$`

= -0.057318