The rewritten expression is 6⁴
Using the rule of logarithm ;
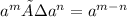
The expression given is ;
The exponent of the numerator = 5
The exponent of the denominator = 1
Subtract the exponents since they have the same base
exponent = 5 - 1 = 4
6⁵/6 =

Hence , the expression is 6⁴