Question

Two years ago, the average number of customers in your all of your company's stores per week was 3173 customers. This figure had increased 6% over the previous two years. Assume that you are doing a current study to test the claim that the mean weekly number of customers is different than it was two years ago. Assume a population standard deviation of 1,550 customers. Suppose you look at a random sample of 73 stores and find an average weekly customer total of 3,391. You wish to test the claim stated above at the 0.10 level. Run the appropriate hypothesis test.

Required:
Write ONLY the conclusion to your hypothesis test.

Answer 1

Accept the null hypothesis

Explanation:

Two years ago, the average number of customers in your all of your company's stores per week was 3173 customers. Assume that you are doing a current study to test the claim that the mean weekly number of customers is different than it was two years ago.

The null hypothesis is:

`H_(0) = 3173`

The alternate hypothesis is:

`H_(A) \\eq 3173`

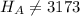
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

Due to our test, we have that
`\mu = 3173`

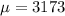
Assume a population standard deviation of 1,550 customers.

This means that
`\sigma = 1550`

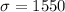
Suppose you look at a random sample of 73 stores and find an average weekly customer total of 3,391.

This means that
`n = 73, X = 3391`

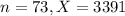
Test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (3391 - 3173)/((1550)/(√(73)))`

`z = 1.24`

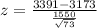
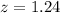
p-value:

Since we are testing if the mean is different of a value, and the z-score is positive, the pvalue is 2 multiplied by 1 subtracted by the pvalue of z = 1.24.

z = 1.24 has a pvalue of 0.9251

2*(1 - 0.9251) = 2*0.0749 = 0.1498

0.1498 > 0.1, which means that we accept the null hypothesis, that is, that the mean weekly number of customers is equal to what it was two years ago at the 0.1 level of significance.