Solution :
Given two resistors :
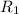 and
and
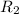 where
where
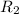 >
>
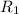
When the resistors are connected in series :
Current,
 .............(1)
.............(1)
When the resistors are connected in series :
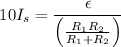
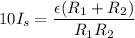 ..................(2)
..................(2)
Therefore, dividing equation (2) by (1), we get

Now, since
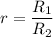 , we have
, we have

∴
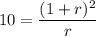
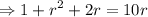
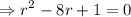
Solving, we get, r = 0.127