Solution :
Let
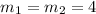 kg
kg
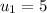 m/s
m/s
Let
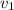 and
and
 are the speeds of the disk
are the speeds of the disk
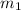 and
and
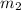 after the collision.
after the collision.
So applying conservation of momentum in the y-direction,
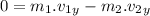
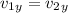
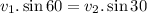
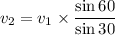
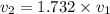
Therefore, the disk 2 have greater velocity and hence more kinetic energy after the collision.
Now applying conservation of momentum in the x-direction,

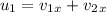
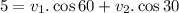
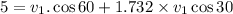
 m/s
m/s
So,
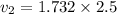
= 4.33 m/s
Therefore, speed of the disk 2 after collision is 4.33 m/s