Question

United Blood Services is a blood bank that serves more than 500 hospitals in 18 states. According to their website, a person with type O blood and a negative Rh factor (Rh-) can donate blood to any person with any bloodtype. Their data show that 43% of people have type O blood and 15% of people have Rh- factor; 52% of people have type O or Rh- factor.

a. Find the probability that a person has both type O blood and the Rh- factor.
b. Find the probability that a person does NOT have both type O blood and the Rh- factor.

Answer 1

a) 0.06 = 6% probability that a person has both type O blood and the Rh- factor.

b) 0.94 = 94% probability that a person does NOT have both type O blood and the Rh- factor.

Explanation:

I am going to solve this question treating these events as Venn probabilities.

I am going to say that:

Event A: Person has type A blood.

Event B: Person has Rh- factor.

43% of people have type O blood

This means that
`P(A) = 0.43`

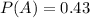
15% of people have Rh- factor

This means that
`P(B) = 0.15`

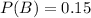
52% of people have type O or Rh- factor.

This means that
`P(A \cup B) = 0.52`

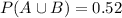
a. Find the probability that a person has both type O blood and the Rh- factor.

This is

`P(A \cap B) = P(A) + P(B) - P(A \cup B)`

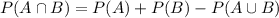
With what we have

`P(A \cap B) = 0.43 + 0.15 - 0.52 = 0.06`

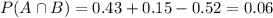
0.06 = 6% probability that a person has both type O blood and the Rh- factor.

b. Find the probability that a person does NOT have both type O blood and the Rh- factor.

1 - 0.06 = 0.94

0.94 = 94% probability that a person does NOT have both type O blood and the Rh- factor.