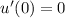Answer:
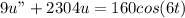
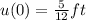 and
and
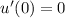
Explanation:
Given
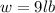 --- weight
--- weight
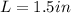 --- stretch
--- stretch
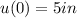 --- initial position
--- initial position
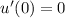 --- initial velocity
--- initial velocity
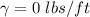 --- no damping
--- no damping
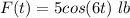 -- External force
-- External force
Required
Solve the initial value problem
The initial value problem is calculated using:
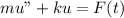
First, convert all lengths to ft
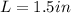
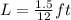
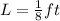
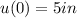
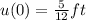
Weight is calculated as:
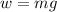 and
and
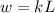
Where
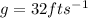
Make m the subject in
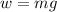
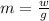
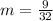
Make k the subject in
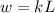
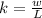
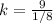
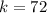
Recall that:
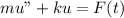
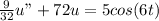
Multiply through by 32
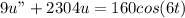
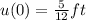 and
and