The graph of the solution set can be seen in option B.
What is a solution set?
The solution set is the set representing all solutions for an equation. It is also the roots that obey a quadratic equation or an inequality.
From the given equation, we have:
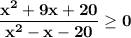
Let's factor out the quadratic equation, we have:
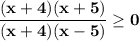
By identifying the intervals;
x ≤ -5 or x > 5
The representation of these intervals on a graduated scale on a number line can be seen in the image attached below.
Therefore, we can conclude that the correct graph that show the solution set to the given equation can be seen in Option B.