Question

Spaulding is the leading maker for basketballs in the US. Spaulding prides itself on the quality that its basketballs have the right amount of bounce when it is taken out of the packaging. They want their product to be ready for use upon opening. The air pressure of a particular ball has a target value of 7.9 PSI. Suppose the basketballs have a normal distribution with a standard deviation of 0.20 PSI. When a shipment of basketballs arrive, the consumer takes a sample of 21 from the shipment and measures their PSI to see if it meets the target value, and finds the mean to be 7.3 PSI. Perform this hypothesis test at the 5% significance level using the critical value approach.

Answer 1

0 < 0.05, which means that we reject the null hypothesis, meaning that the air pressure of the balls is different of the target value of 7.9.

Explanation:

The air pressure of a particular ball has a target value of 7.9 PSI.

This means that the null hypothesis is:

`H_(0): \mu = 7.9`

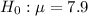
The alternate hypothesis is:

`H_(a): \mu \\eq 7.9`

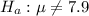
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

The hypothesis tested means that
`\mu = 7.9`

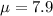
Suppose the basketballs have a normal distribution with a standard deviation of 0.20 PSI.

This means that
`\sigma = 0.2`

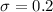
When a shipment of basketballs arrive, the consumer takes a sample of 21 from the shipment and measures their PSI to see if it meets the target value, and finds the mean to be 7.3 PSI.

This means that
`X = 7.3, n = 21`

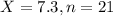
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (7.3 - 7.9)/((0.2)/(√(21)))`

`z = -13.74`

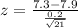
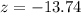
pvalue:

We are testing that the mean pressure is different than the target value of 7.9, and since the test statistic is negative, the pvalue is 2 multiplied by the pvalue of z = -13.74, which we find looking at the z-table.

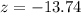`z = -13.74` has a pvalue of 0.

2*0 = 0

0 < 0.05, which means that we reject the null hypothesis, meaning that the air pressure of the balls is different of the target value of 7.9.