Answer:
D)
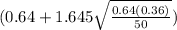
90 percent confidence interval for the proportion of all students in her district who read at least 1 book last month
(0.52846 , 0.75166)
Explanation:
Step:-1
Given that the random sample size 'n' = 50
The sample proportion
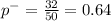
90 percent confidence interval for the proportion of all students in her district who read at least 1 book last month
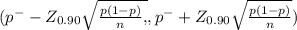
Step(ii):-
Level of significance = 0.90
Z₀.₉₀ = 1.645

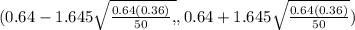
(0.64 -1.645(0.06788) , (0.64 + 1.645(0.06788)
(0.52846 , 0.75166)
Final answer:-
90 percent confidence interval for the proportion of all students in her district who read at least 1 book last month
(0.52846 , 0.75166)