Question

Which function would you use to find to find the measurement of angle D?PLEASE HELP ME​

Answer 1

D.

Explanation:

Note that with respect to ∠D, its adjacent side is f and the hypotenuse is e.

Since we are given the adjacent side and its hypotenuse, we can use cosine. Recall that cosine is the following ratio:

`\displaystyle \cos(\theta)=\frac{\text{adjacent}}{\text{hypotenuse}}`

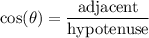
So, for ∠D, this yields that:

`\displaystyle \cos(D)=(f)/(e)`

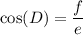
To solve for D, then, we can take the inverse cosine of both sides:

`\displaystyle m\angle D=\cos^(-1)\Big((f)/(e)\Big)`

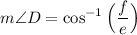
Our answer is D.