Answer:
a) There are 93,367,432,000,000 ways to place the lunch order.
b) There are 11,861,676,000,000 ways for the company to place the lunch order if the 10 lunches purchased are all different.
Explanation:
Permutations formula:
The number of possible permutations of x elements from a set of n elements is given by the following formula:
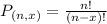
a. How many different ways are there for the company to place the lunch order for the 10 lunches?
For each of the 10 lunches, there are 25 options. So
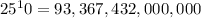
There are 93,367,432,000,000 ways to place the lunch order.
b. How many ways are there for the company to place the lunch order if the 10 lunches purchased are all different?
The order is important, which means that the permutations formula is used to solve this question. So
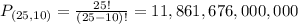
There are 11,861,676,000,000 ways for the company to place the lunch order if the 10 lunches purchased are all different.