Answer:
a,b) #_ {electron} = 1.64 10¹⁹ electrons, c) R = 19.54 Ω, d) V = 10.3 V
Step-by-step explanation:
a and b) The current is defined as the number of electrons that pass per unit of time
let's look for the load
Q = I t
Q = 0.526 5
Q = 2.63 C
Let's use a direct rule of three proportions. If an electron has a charge of 1.6 10⁻¹⁹ C, how many electrons does 2.63 C have?
#_ {electron} = 2.63 C (1 electron / 1.6 10⁻¹⁹)
#_ {electron} = 1.64 10¹⁹ electrons
c) the resistance of a wire is given by
R = ρ l / A
where the resistivity of tungsten is 5.6 10⁻⁸ Ω
the area of the wire is
A = π r2 = π d²/4
we substitute
R =

let's calculate
R = 5.6 10⁻⁸ 0.580
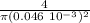
R = 19.54 Ω
d) let's use ohm's law
V = i R
V = 0.526 19.54
V = 10.3 V