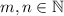Answer:
(i) La raíz enésima de un producto de dos números es igual al producto de las raíces enésimas de cada número del producto:
![\sqrt[n]{a\cdot b} = \sqrt[n] {a}\cdot \sqrt [n] {b}](https://img.qammunity.org/2022/formulas/mathematics/high-school/o7gaji5ksf9b3l4ktmcyx2rfhp0toxscck.png) ,
,
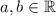 ,
,
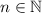
(ii) La raíz enésima de una división entre dos números es igual a la división de la raíz enésima del numerador y la raíz enésima del denominador:
![\sqrt [n]{(a)/(b) } =\frac{\sqrt[n]{a}}{\sqrt [n] {b}}](https://img.qammunity.org/2022/formulas/mathematics/high-school/gjgqro4vab5culll49nxynrati9da9i8xf.png) ,
,
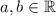 ,
,
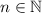
(iii) La raíz emésima de la raíz enésima de un número es igual a la raíz eme-enésima del número:
![\sqrt[m]{\sqrt[n]{a} } = \sqrt[m\cdot n]{a}](https://img.qammunity.org/2022/formulas/mathematics/high-school/jdti3h53nema0fxs3lfgeakn27c4gp5i22.png) ,
,
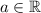 ,
,
Explanation:
Existen tres propiedades fundamentales de la radicación, las cuales se enumeran a continuación:
(i) La raíz enésima de un producto de dos números es igual al producto de las raíces enésimas de cada número del producto:
![\sqrt[n]{a\cdot b} = \sqrt[n] {a}\cdot \sqrt [n] {b}](https://img.qammunity.org/2022/formulas/mathematics/high-school/o7gaji5ksf9b3l4ktmcyx2rfhp0toxscck.png) ,
,
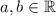 ,
,
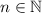
(ii) La raíz enésima de una división entre dos números es igual a la división de la raíz enésima del numerador y la raíz enésima del denominador:
![\sqrt [n]{(a)/(b) } =\frac{\sqrt[n]{a}}{\sqrt [n] {b}}](https://img.qammunity.org/2022/formulas/mathematics/high-school/gjgqro4vab5culll49nxynrati9da9i8xf.png) ,
,
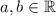 ,
,
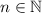
(iii) La raíz emésima de la raíz enésima de un número es igual a la raíz eme-enésima del número:
![\sqrt[m]{\sqrt[n]{a} } = \sqrt[m\cdot n]{a}](https://img.qammunity.org/2022/formulas/mathematics/high-school/jdti3h53nema0fxs3lfgeakn27c4gp5i22.png) ,
,
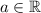 ,
,