Answer:
- The sum of the series = 198.
Explanation:
In the given arithmetic series,
- The first term (a) = 6
- Common difference (d) = (aₙ – aₙ₋₁) = 10 - 6 = 4
- Last term (aₙ) = 38
To find the sum of the series, we need to find the number of terms (n) at first. So,
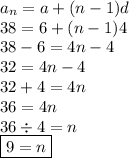
Now, let's find the sum of the arithmetic series (Sₙ).
![S_(n) = (n)/(2) [2a + (n - 1)d]\\S_(n) = (9)/(2) [2*6 + (9 -1)4]\\S_(n) = (9)/(2) [12+ (8*4)]\\S_(n) = (9)/(2) [12+ 32]\\S_(n) = (9)/(2) (44)\\S_(n) = 9*22\\\boxed{S_(n) = 198}](https://img.qammunity.org/2023/formulas/mathematics/high-school/g2jvmvwicj4fw8jlficvccj7vc9m4opaum.png)
- The sum of the series = 198.
_______________
Hope it helps!