The volume of the shaded portion in the composite figure, excluding the cone inside a triangular pyramid, is
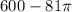 units³. Thus, the correct answer is (D)
units³. Thus, the correct answer is (D)
 units³.
units³.
To find the volume of the shaded portion, we need to calculate the volume of the triangular pyramid and subtract the volume of the cone.
1. Volume of Triangular Pyramid:
![\[ V_{\text{pyramid}} = (1)/(3) * \text{Base Area} * \text{Height} \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/vedqgme7fh2zm40r4pbmekufjp8z4piqfo.png)
The base of the triangular pyramid is a rectangle with dimensions
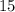 and 10, so the base area is
and 10, so the base area is
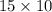 . The height of the pyramid is
. The height of the pyramid is
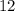 .
.
![\[ V_{\text{pyramid}} = (1)/(3) * (15 * 10) * 12 \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/n209tiqnau510xlj16beh7xtlp3otuf2lw.png)
2. Volume of Cone:
![\[ V_{\text{cone}} = (1)/(3) \pi r^2 h \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/yiwt1gnp1919q81a3blawt3i8duy8wz759.png)
The diameter of the cone is 9, so the radius r is
 . The height \( h \) is 12.
. The height \( h \) is 12.
![\[ V_{\text{cone}} = (1)/(3) \pi \left((9)/(2)\right)^2 * 12 \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/gn9ln527xr4sapgo595t66736wz374k7lm.png)
Now, subtract the volume of the cone from the volume of the pyramid to get the volume of the shaded portion:
![\[ \text{Volume of Shaded Portion} = V_{\text{pyramid}} - V_{\text{cone}} \]\[ \text{Volume of Shaded Portion} = \left((1)/(3) * (15 * 10) * 12\right) - \left((1)/(3) \pi \left((9)/(2)\right)^2 * 12\right) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/7zq6rllepkl308dbtk2ezjec1j7hxz7wwl.png)
Now, simplify this expression to get the final answer.
![\[ \text{Volume of Shaded Portion} = (600 - 81 \pi) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/zo0se919utbxwq7or8omzrc8to7vhpw0q7.png)
Therefore, the correct answer is option (D)
 units³.
units³.