Question

Data on pull-off force (pounds) for connectors used in an automobile engine application are as follows:

79.6 75.1 78.2 74.1 73.9 75.0 77.6 77.3 73.8 74.6 75.5 74.0 74.7 75.9 72.7 73.8 74.2 78.1 75.4 76.3 75.3 76.2 74.9 78.0 75.1 76.8

If necessary, round all intermediate calculations to four decimal places (e.g. 12.3456).

Required:
a. Calculate a point estimate of the mean pull-off force of all connectors in the population. State which estimator you used and why?
b. Calculate a point estimate of the pull-off force value that separates the weakest 50% of the connectors in the population from the strongest 50%.
c. Calculate point estimates of the population variance and the population standard deviation.
d. Calculate the standard error of the point estimate found in part (a). Interpret the standard error.
e. Calculate a point estimate of the proportion of all connectors.

Answer 1

a. A point estimate of the mean pull-force of all connectors in the population is approximately 75.7385

The point estimate for the mean used is the sample mean

b. The point estimate of the pull force that separates the weakest 50% of the connectors from the strongest 50% is 74.3131 N

c. The point estimate of the population variance is approximately 2.8577

The point estimate for the population standard deviation is approximately 1.6905

d. The standard error of the mean is approximately 0.3315

e. The point estimate of a proportion of the connectors are;

(72.7, 0.0385) , (73.8, 0.0769) , (73.9, 0.0385) , (74, 0.0385) , (74.1, 0.0385) ,(74.2, 0.0385), (74.6, 0.0385) , (74.7, 0.0385) , (74.9, 0.0385) , (75.1, 0.0769) , (75.3, 0.0385) , (75.4, 0.0385) , (75.5, 0.0385) , (75.6, 0.0385) , (75.8, 0.0385) , (76.2, 0.0385) , (76.3, 0.0385) , (76.8, 0.0385) , (77.3, 0.0385) , (77.6, 0.0385) , (78, 0.0385) , (78.1, 0.0385) , (78.2, 0.0385) , (79.6, 0.0385)

Explanation:

The given data for the pull-force (pounds) for connectors used in an automobile engine are presented as follows;

Pull-force (pounds); 79.6, 75.1, 78.2, 74.1, 73.9, 75.6, 77.6, 77.3, 73.8, 74.6, 75.5, 74.0, 74.7, 75.8, 72.7, 73.8, 74.2, 78.1, 75.4, 76.3, 75.3, 76.2, 74.9, 78.0, 75.1, 76.8

a. A point estimate of the mean pull-force of all connectors in the population is the sample mean given as follows;

`Mean, \ \overline x = (\Sigma x_i)/(n)`

`\Sigma x_i` = The sum of the data = 1966.6

n = The sample size = 26

Therefore, the sample mean,
`\overline x` = 1966.6/26 ≈ 75.7385

The point estimate for the mean is approximately 75.7385

The sample mean was used as the point estimate for the mean because it is simple and representative of the sample

b. The weakest 50% of the connectors are;

72.7, 73.8, 73.8, 73.9, 74, 74.1, 74.2, 74.6, 74.7, 74.9, 75.1, 75.1, 75.3

The sum of forces that separates the weakest 50%,
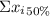`\Sigma x_(i)_(50 \%)` = 966.2

The point estimate of the pull force that separates the weakest 50% of the connectors from the strongest 50% =
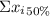`\Sigma x_(i)_(50 \%)`/13 = 966.2/13 = 74.3131 N

c. The estimate of the population variance is the sample variance, given as follows;

`s^2 =(\sum \left (x_i-\overline x \right )^(2) )/(n - 1)}`

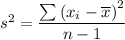
Where;

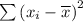`{\sum \left (x_i-\overline x \right )^(2) }` ≈ 71.4415

Therefore;

`s^2 =(71.4415 )/(25)} \approx 2.8577`

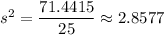
The point estimate of the population variance, s², is 2.8577

The point estimate for the population standard deviation, σ, is tha sample standard deviation, 's', given as follows;

s = √s² = √2.8577 ≈ 1.6905

The point estimate for the population standard deviation ≈ 1.6905

d. The standard error of the mean is given as follows;

`SE_(\mu_x) = (s)/(√(n) )`

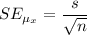
Therefore, we have;

`SE_(\mu_x)` = 1.6905/√(26) ≈ 0.3315

The standard error indicates the likely hood of the difference between the sample mean and the population mean

e. The point estimate of a proportion of the connectors are;

(Number of sample with a given pull-force value)/(Sample size (26))

Therefore, using Microsoft Excel, we have

(72.7, 0.0385) , (73.8, 0.0769) , (73.9, 0.0385) , (74, 0.0385) , (74.1, 0.0385) ,(74.2, 0.0385), (74.6, 0.0385) , (74.7, 0.0385) , (74.9, 0.0385) , (75.1, 0.0769) , (75.3, 0.0385) , (75.4, 0.0385) , (75.5, 0.0385) , (75.6, 0.0385) , (75.8, 0.0385) , (76.2, 0.0385) , (76.3, 0.0385) , (76.8, 0.0385) , (77.3, 0.0385) , (77.6, 0.0385) , (78, 0.0385) , (78.1, 0.0385) , (78.2, 0.0385) , (79.6, 0.0385)