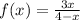
First Method: Using Graph
Finding the limits as x approaches infinity and negative infinity is one way to solve this problem. As x reaches infinity, simply follow the graph line (colored purple) to the far right to find its limit. If we trace it, we can see that the Y value never exceeds -3 (orange), indicating that the limit is equal to -3 as x approaches infinity. You'd do the same with negative infinity, the limit is -3. We may now say the following:
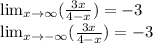
And that's the answer to your question.
Second Method: Using Mathematics
I'm not sure if this solution is suitable for your stage, but you can solve this problem using L'Hopital's rule:

Graphed by: Desmos