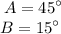Answer:
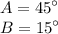
Explanation:
we are given two equation and condition
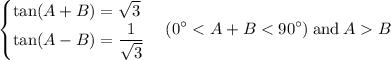
let's work with first equation
recall unit circle so A and B should be in Q:I
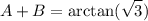
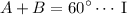
let's work with second equation:
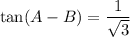
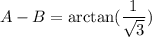
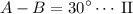
now let's use elimination method to figure out A and B
to do so combine equation I and II
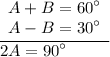
divide both sides by 2:
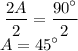
substitute the value of A to the second equation:
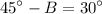
cancel 60° from both sides:
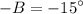
divide both sides by -1
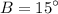
hence,