Question

4. The graph of h(x) = x^2 was transformed to create the graph of k(x) = -4x^2? Which of these describes the transformation from the graph of h to the graph

of k? A.) A reflection over the x-axis and a vertical
stretch
B.) A reflection over the x-axis and a vertical
compression
C.) A reflection over the y-axis and a vertical
compression
D.) A reflection over the y-axis and a vertical stretch

Answer 1

A. A reflection over the x-axis and a vertical stretch.

Explanation:

Let
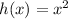`h(x) = x^(2)`, to obtain
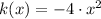`k(x) = -4\cdot x^(2)`, we need to use the following two operations:

(i) Vertical stretch

`g(x) = k\cdot f(x)`,
`k\in \mathbb{R}^(+)`

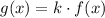(ii) Reflection over the x-axis

`g(x) = -f(x)`

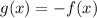
Let prove both transformations in
`h(x)`:

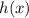Step 1 - Vertical stretch (
`k = 4`)

`h'(x) = 4\cdot x^(2)`

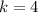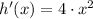
Step 2 - Reflection over the x-axis

`k(x) = -4\cdot x^(2)`

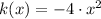
Hence, correct answer is A.