Question

4) An arithmetic sequence has a 7th term of 54 and a 13th term of 94. Find the common difference

(Write as a fraction)
Plz help

Answer 1

a = 14 and d = 6.67

Explanation:

The nth term of an AP is given by :

`a_n=a+(n-1)d`

Where

a is the first term and d is the common difference

ATQ,

An arithmetic sequence has the 7th term of 54 and the 13th term of 94 i.e.

`a+6d=54\ ......(1)\\\\a+12d=94\ ........(2)`

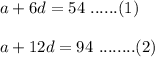
Subtract equation (2) from (1).

a+6d-(a+12d) = 54-94

a+6d-a-12d = -40

-6d = -40

d = 6.67

Put the value of d in equation (1).

`a+6(6.666)=54\\\\a=54-39.96\\\\a=14.04`

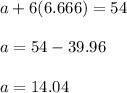
or

a = 14

Hence, the first term is 14 and the common difference is 6.67.