Answer:
m∠ACB = 49.88°
Explanation:
From the figure attached,
Measure of wire AC attached to the top 'C' of the building BC = 340 m
Horizontal distance between the base 'B' of the building and point A = 260 m
Angle of depression = ∠ACB
By applying sine rule in the given triangle,
sin(∠ACB) =
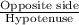
=
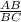
=
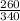
m∠ACB =
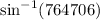
= 49.88°