Question

Robin hood plans to use a 54 ft ladder to reach the castle window of Maid Marian. Little John, who made the ladder, advised Robin that the angle of elevation of the ladder must be between \displaystyle 55^{of}55 o and \displaystyle 70^{of}70 o for safety. What are the minimum and maximum heights that can safely by reached by the top of the ladder when it is placed against the 50 ft castle wall

Answer 1

The minimum height is: 44.24 ft and the maximum is 50.74ft

Explanation:

Given

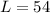`L = 54` --- Length of ladder

`55 \le \theta \le 70`

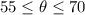
Required

The minimum and maximum height

The question is illustrated with the attached image:

The height h is calculated using:

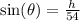`\sin(\theta) = (h)/(54)` --- sine equation

When
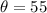`\theta = 55`, we have:

`\sin(55) = (h)/(54)`

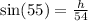
Make h the subject

`h = 54 * \sin(55)`

`h = 54 * 0.8192`

`h = 44.24ft`

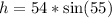
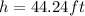
When
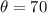`\theta = 70`, we have

This gives:

`\sin(70) = (h)/(54)`

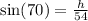
Make h the subject

`h = 54 * \sin(70)`

`h = 54 * 0.9397`

`h = 50.74ft`

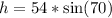
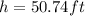
The minimum height is: 44.24 ft and the maximum is 50.74ft