The question is incomplete. The complete question is :
Jaina and Tomas compare their compound interest accounts to see how much they will have in the accounts after three years. They substitute their values shown below into the compound interest formula. Compound Interest Accounts Name Principal Interest Rate Number of Years Compounded Jaina $300 7% 3 Once a year Tomas $400 4% 3 Once a year. Which pair of equations would correctly calculate their compound interests?
Solution :
It is given that Jaina and Tomas wants to open an account by depositing a principal amount for a period of 3 years and wanted to calculate the amount they will have using the compound interest formula.
So for Jiana :
Principal, P = $300
Rate of interest, r = 7%
Time, t = 3
Compounded yearly
Therefore, using compound interest formula, we get
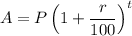
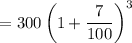

Now for Tomas :
Principal, P = $400
Rate of interest, r = 4%
Time, t = 3
Compounded yearly
Therefore, using compound interest formula, we get
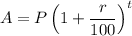

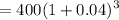
Therefore, the pair of equations that would correctly calculate the compound interests for Jaina is
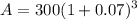 .
.
And the pair of equations that would correctly calculate the compound interests for Tomas is
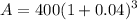 .
.