Answer:
0.0384 < 0.05, which means that we can conclude that the mean amount of time that college students spend in the shower is significantly different from 5 minutes.
Explanation:
A facilities manager at a university reads in a research report that the mean amount of time spent in the shower by an adult is 5 minutes.
This means that the null hypothesis is
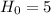
He decides to collect data to see if the mean amount of time that college students spend in the shower is significantly different from 5 minutes.
This means that the alternate hypothesis is
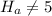
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
Null hypothesis:
Tests
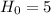 , which means that
, which means that
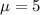
In a sample of 8 students, he found the average time was 5.55 minutes and the standard deviation was 0.75 minutes.
This means, respectively, that
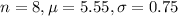
Test statistic:
The test statistic is:

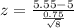
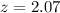
Pvalue:
Since we are testing if the mean is different from a value, and z is positive. The pvalue is two multiplied by 1 subtracted by the pvalue of z = 2.07.
z = 2.07 has a pvalue of 0.9808
2*(1 - 0.9808) = 2*(0.0192) = 0.0384
Decision:
0.0384 < 0.05, which means that we can conclude that the mean amount of time that college students spend in the shower is significantly different from 5 minutes.