Question

Suspecting that television repair shops tend to charge women more than they do men, Emily disconnected the speaker wire on her portable television and took it to a sample of 12 shops. She was given repair estimates that averaged $85, with a standard deviation of $28. Her friend John, taking the same set to another sample of 9 shops, was provided with an average estimate of $65, with a standard deviation of $21. Assuming normal populations with equal standard deviations, What is the the pooled estimate of the common variance with the 0.05 level

Answer 1

The pooled estimate of the common variance is approximately 639.59

Explanation:

The given parameters are;

The number of shops Emily visited, n₁ = 12 shops

The average repair estimate Emily was given,
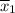`\overline x_1` = $85

The standard deviation of the estimate Emily was given, s₁ = $28

The number of shops John visited, n₂ = 9 shops

The average repair estimate John was given,
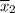`\overline x_2` = $65

The standard deviation of the estimate John was given, s₂ = $21

The pooled estimate of the common variance,
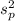`s_p^2`, is given as follows;

`s_p^2 = ((n_1 - 1)\cdot s_1^2+(n_2 - 1)\cdot s_2^2)/(n_1 + n_2-2)`

`\therefore s_p^2 = ((12 - 1)\cdot 28^2+(9 - 1)\cdot 21^2)/(12 + 9-2) = 639.578947368`

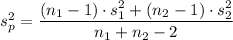
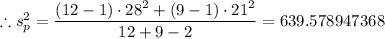
∴ The pooled estimate of the common variance,
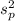`s_p^2`, ≈ 639.59