Question

A genetic experiment with peas resulted in one sample of offspring that consisted of green peas and yellow peas.444167a. Construct a %confidence interval to estimate of the percentage of yellow peas.90b. It was expected that 25% of the offspring peas would be yellow. Given that the percentage of offspring yellow peas isnot 25%, do the results contradict expectations

Answer 1

Answer: a.) 0.2438 < p < 0.3028

b.) No

Step-by-step explanation: Confidence Interval to estimate the percentage of yellow peas is calculated following these steps:

1) Total of the offspring in one sample:

n = 444 + 167

n = 611

2) Proportion of yellow peas, which is the number of yellow peas observed divided by the total of offspring:

p =
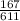`(167)/(611)` = 0.2733

3) For a 90% confidence interval:

α = 1 - 0.90

`z_(\alpha/2)=z_(0.05)`

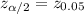
Checking z-table, z-score will be: z = 1.645.

4) Calculate margin of error:

`E=z.\sqrt{(p(1-p))/(n) }`

`E=1.645.\sqrt{(0.27(1-0.27))/(611) }`

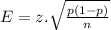
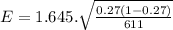
E = 0.0295

5) Confidence interval has boundaries:

p - E = 0.2733 - 0.0295 = 0.2438

p + E = 0.2733 + 0.0295 = 0.3028

Then, we are 90% confident that the percentage of yellow peas is between 24.38% and 30.28%.

b.) Since 25% is in the confidence interval, and we are 90% sure the true percentage of yellow peas are inside the interval, the result does not contradict the expectations.