Answer:
a) F = 64.30 N, b) θ = 121.4º
Step-by-step explanation:
Forces are vector quantities so one of the best methods to add them is to decompose each force and add the components
let's use trigonometry
Force F1
sin 170 = F_{1y} / F₁
cos 170 = F₁ₓ / F₁
F_{1y} = F₁ sin 170
F₁ₓ = F₁ cos 170
F_{1y} = 100 sin 170 = 17.36 N
F₁ₓ = 100 cos 170 = -98.48 N
Force F2
sin 30 = F_{2y} / F₂
cos 30 = F₂ₓ / F₂
F_{2y} = F₂ sin 30
F₂ₓ = F₂ cos 30
F_{2y} = 75 sin 30 = 37.5 N
F₂ₓ = 75 cos 30 = 64.95 N
the resultant force is
X axis
Fₓ = F₁ₓ + F₂ₓ
Fₓ = -98.48 +64.95
Fₓ = -33.53 N
Y axis
F_y = F_{1y} + F_{2y}
F_y = 17.36 + 37.5
F_y = 54.86 N
a) the magnitude of the resultant vector
let's use Pythagoras' theorem
F = Ra Fx ^ 2 + Fy²
F = Ra 33.53² + 54.86²
F = 64.30 N
b) the direction of the resultant
let's use trigonometry
tan θ’= F_y / Fₓ
θ'=
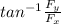
θ'= tan⁻¹ (54.86 / (33.53)
θ’= 58.6º
this angle is in the second quadrant
The angle measured from the positive side of the x-axis is
θ = 180 -θ'
θ = 180- 58.6
θ = 121.4º