Answer:
Explanation:
Average price of a two bedroom apartment can be approximated by the equation,
p(t) =
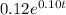
Here, t represents the duration from year 1994.
Duration from year 1994 to year 2004 = 10 years
p(10) =
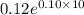
= 0.12e
= 0.3262
≈ 0.33 million
Cost of the apartment in 2004 was 0.33 million.
Let the equation to calculate the rate of increase in the price is,
p(t) =

Cost of the apartment after 10 years = 0.33
0.33 =
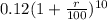
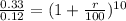
2.75 =
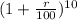

1 +
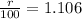
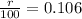
r = 10.6%
Therefore, price of the apartment is increasing with 10.6%