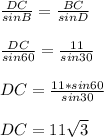Question

Please help!!! (Ignore the AD it’s actually supposed to be DC)

Answer 1

BD = 22, DC = 11√3

Explanation:

In triangle ABC, ∠B = 45°, ∠C = 90°. Hence:

∠A + ∠B + ∠C = 180° (sum of angles in a triangle)

∠A + 45 + 90 = 180

∠A + 135 = 180

∠A = 45°

Using sine rule to find BC:

`(BC)/(sinA)=(AB)/(sinC) \\\\(BC)/(sin45)=(11√(2) )/(sin90) \\\\BC=(11√(2)*sin45 )/(sin90) \\BC=11`

In triangle BCD, ∠D = 30°, ∠C = 90°. Hence:

∠D + ∠B + ∠C = 180° (sum of angles in a triangle)

∠B + 30 + 90 = 180

∠B + 120 = 180

∠B = 60°

Using sine rule to find BD:

`(BD)/(sinC)=(BC)/(sinD) \\\\(BD)/(sin90) =(11)/(sin30) \\\\BD=(11*sin90)/(sin30)\\\\BD=22`

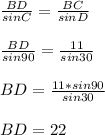
Using sin rule to find DC:

`(DC)/(sinB)=(BC)/(sinD) \\\\(DC)/(sin60) =(11)/(sin30) \\\\DC=(11*sin60)/(sin30)\\\\DC=11√(3)`