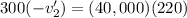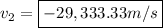Question

A 40,000kg rocket traveling at 220 m/s expels 300kg worth of gases at what velocity?

Answer 1

Hi there!

We can use the conservation of momentum to solve.

`m_1v_1 + m_2v_2 = m_1v_1' + m_2v_2'`

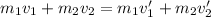
m1 = mass of rocket (40,000 kg)

m2 = mass of gas (300 kg)

v1, v2 = INITIAL velocities of rocket and gas (0 m/s)

v1' = FINAL velocity of rocket (+220 m/s, assuming UP to be positive)

v2' = FINAL velocity of gas (- ? m/s, DOWNWARD so negative)

This is an example of a "recoil" collision, so:

`0 = m_1v_1' + m_2(v_2')`

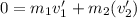
Set the two equal:

`m_2(-v_2') = m_1v_1'`

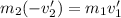
Plug in the givens:

`300(-v_2') = (40,000)(220)\\\\`

`\v_2 = \boxed{-29,333.33 m/s}`
`v_2 = \boxed{-29,333.33 m/s}`