Answer:
99% of the sample means will fall between 0.93288 and 0.94112.
Explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
 and standard deviation
and standard deviation
 , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
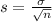 .
.
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
The true mean is .9370 with a standard deviation of 0.0090
This means that
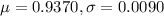
Sample of 32:
This means that
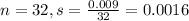
Within what interval will 99 percent of the sample means fall?
Between the 50 - (99/2) = 0.5th percentile and the 50 + (99/2) = 99.5th percentile.
0.5th percentile:
X when Z has a pvalue of 0.005. So X when Z = -2.575.

By the Central Limit Theorem
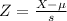
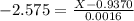

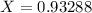
99.5th percentile:
X when Z has a pvalue of 0.995. So X when Z = 2.575.
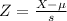
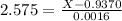
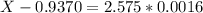
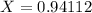
99% of the sample means will fall between 0.93288 and 0.94112.