Answer:
20
Explanation:
firstly let's find out the side lengths of the triangle using formula
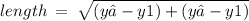
length of AB
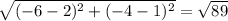
length of AC
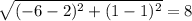
length of BC

Now we have all three side lengths:
a =√89 b = 8 and c = 5
using this formula to find the semi perimeter where a, b and c are the side lengths, input them in
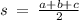
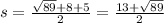
Use heron's formula
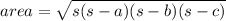
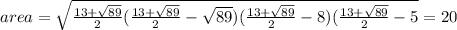
area = 20