Question

What is the area of a triangle with vertices at (−4, −6), (1, −6), and (1, 2)?

Answer 1

20

Explanation:

firstly let's find out the side lengths of the triangle using formula

`length \: = \: √((y₂-y1) + ( y₂-y1))`

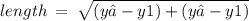
length of AB

`\sqrt{( - 6 - 2) {}^(2) + ( - 4 - 1) {}^(2) } = √(89)`

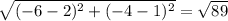
length of AC

`\sqrt{( - 6 - 2) {}^(2) + (1 - 1) {}^(2) } = 8`

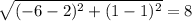
length of BC

`\sqrt{( - 6 - ( - 6)) {}^(2) + (1 - ( - 4)) {}^(2) } = 5`

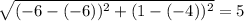
Now we have all three side lengths:

a =√89 b = 8 and c = 5

using this formula to find the semi perimeter where a, b and c are the side lengths, input them in

`s \: = \: (a + b + c)/(2)`

`s = ( √(89) + 8 + 5 )/(2) = \frac{13 + √(89) } {2}`

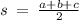
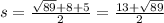
Use heron's formula

`area = √(s(s - a)(s - b)(s - c))`

`area = \sqrt{ (13 + √(89) )/(2)((13 + √(89) )/(2) - √(89))( (13 + √(89) )/(2) - 8)((13 + √(89) )/(2) - 5 } = 20`

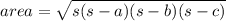
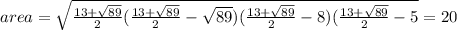
area = 20