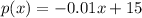Question

A movie theater has been charging $10.00 per person and selling about 500 tickets on a typical weeknight. After surveying their customers, the theater management estimates that for every 50 cents that they lower the price, the number of moviegoers will increase by 50 per night. Find the demand function. (Let x represent the number of tickets sold and p represent the price.)

Answer 1

`p(x) = -0.01x + 15`

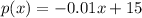
Explanation:

Given

Let x represent the number of tickets, and p the charges

`(x_1,p_1) = (500,10)`

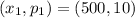
A reduction of 50c gives an increment of 50 tickets.

This gives:

`(x_2,p_2) = (500+50,10-0,5)` ----
`50c = \$0.5`

`(x_2,p_2) = (550,9.5)`

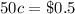
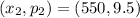
Required

Determine the demand function

First, calculate the slope:

`m = (p_2 - p_1)/(x_2 - x_1)`

`m = (9.5 - 10)/(550-500)`

`m = (-0.5)/(50)`

`m = -0.01`

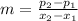
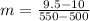
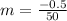
So, the equation is:

`p = m(x - x_1) + y_1`

`p = -0.01(x - 500) +10`

`p = -0.01x + 5 +10`

`p = -0.01x + 15`

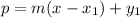
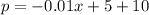
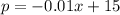
Hence, the function is:

`p(x) = -0.01x + 15`