Answer:
Question 11:

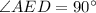
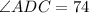
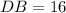
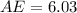
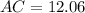
Question 12:
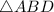 ,
,
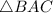 ,
,
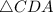 and
and
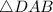
Question 13:
AC and BD are perpendicular lines, and they are diagonals
Explanation:
Question 11
Given

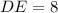
See attachment for Rhombus
Required
Determine the indicated sides
Solving (a):
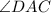
Diagonal CA divides
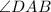 into 2 equal angles
into 2 equal angles
i.e
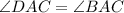
So:

Solving (b):
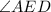
The angles at E is 90 degrees because diagonals AC and BD meet at a perpendicular.
So:
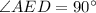
Solving (c):
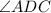
First, we calculate
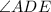 , considering
, considering
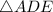 :
:
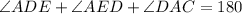
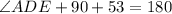
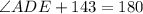
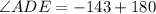
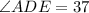
To calculate
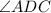 , we have:
, we have:
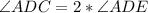
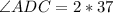
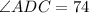
Solving (d):
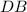
From the rhombus
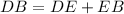
Where
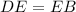
So:

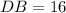
Solving (e):
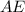
To do this we consider
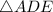
Using the tan formula
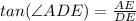
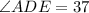 and
and
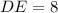
So:
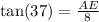
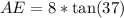
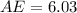
Solving (f):
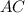
This is calculated as:
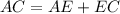
Where
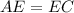
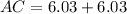
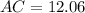
Question 12: Isosceles Triangle
In the rhombus, all 4 sides are equal;
So, the isosceles triangle are:
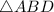 ,
,
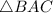 ,
,
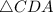 and
and
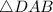
Question 13:
AC and BD are perpendicular lines, and they are diagonals