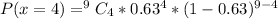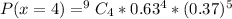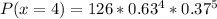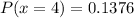Complete question:
On the package for a certain brand of spinach seeds there is a guarantee that, if the printed instructions are followed, 63% of planted seeds will germinate. A random sample of 9 seeds is chosen. If these seeds are planted according to the instructions, find the probability that 4 of them germinate.
Answer:
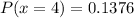
Explanation:
Given
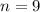
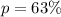 --- proportion that germinates
--- proportion that germinates
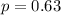
Required
P(x = 4)
This question follows a binomial distribution:

When x = 4;