Question

Your engineering position requires frequent travel to the west coast, typically through Chicago. In reviewing historical airline data, you have determined that over the last year flights into Chicago on Southwest have been normally distributed, arriving an average of 72.3 minutes late with a standard deviation of 9.8 minutes. Yesterday, a travel agent informed you that Southwest recently changed their scheduling into Chicago and has improved arrival times. To confirm this claim, you collect the arrival times for a random sample of 47 Southwest flights arriving into Chicago, and find a sample mean of 70.7 minutes and a sample standard deviation of 7.1 minutes. Has there been a change in the mean arrival times on Southwest

Answer 1

The given data does not support the submission that there has been a change in the mean arrival times on Southwest

Explanation:

The known mean late arrival time, μ = 72.3

The known standard deviation in late arrival time, σ = 9.8 minutes

The number of flights in the sample, n = 47

The sample mean late arrival time,
`\overline x` = 70.7

The sample standard deviation late arrival time, s = 7.1

Using a significance level of 0.01

The null hypothesis is, H₀ ; μ = 70.7

The alternative hypothesis is, Hₐ ; μ ≠ 70.7

The test statistic is given as follows;

`z=\frac{\bar{x}-\mu }{(\sigma )/(√(n))}`

`z=(70.7-72.3 )/((9.8 )/(√(47))) \approx -1.119290547`

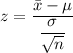
∴ z ≈ -1.12

p-value = 2 × P(z < -1.12) = 2 × 0.13136 = 0.26272

Given that the p-value of 0.26272 is larger than the significance level, 0.05, we fail to reject the null hypothesis

Therefore, there is not enough statistical evidence to show that there has been a change in the mean arrival times on Southwest