Answer:
The volume of the cone is changing at a rate of approximately 8670.796 cubic inches per second.
Explanation:
Geometrically speaking, the volume of the right circular cone (
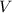 ), in cubic inches, is defined by the following formula:
), in cubic inches, is defined by the following formula:
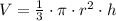 (1)
(1)
Where:
 - Radius, in inches.
- Radius, in inches.
 - Height, in inches.
- Height, in inches.
Then, we derive an expression for the rate of change of the volume (
 ), in cubic inches per second, by derivatives:
), in cubic inches per second, by derivatives:
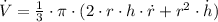 (2)
(2)
Where:
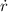 - Rate of change of the radius, in inches per second.
- Rate of change of the radius, in inches per second.
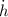 - Rate of change of the height, in inches per second.
- Rate of change of the height, in inches per second.
If we know that
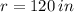 ,
,
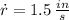 ,
,
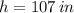 and
and
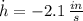 , then the rate of change of the volume is:
, then the rate of change of the volume is:
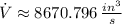
The volume of the cone is changing at a rate of approximately 8670.796 cubic inches per second.