Question

A 8.73-g bullet is moving horizontally with a velocity of 345 m/s, where the sign indicates that it is moving to the right (see part a of the drawing). The bullet is approaching two blocks resting on a horizontal frictionless surface. Air resistance is negligible. The bullet passes completely through the first block (an inelastic collision) and embeds itself in the second one, as indicated in part b. Note that both blocks are moving after the collision with the bullet. The mass of the first block is 1201 g, and its velocity is 0.714 m/s after the bullet passes through it. The mass of the second block is 1606 g. (a) What is the velocity of the second block after the bullet imbeds itself

Answer 1

v₃ = 1.334 m/s

Step-by-step explanation:

This problem can be solved using the law of conservation of momentum:

`m_(1)u_(1) + m_(2)u_(2) + m_(3)u_(3) = m_(1)v_(1) + m_(2)v_(2) + m_(3)v_(3)\\`

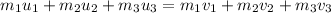
m₁ = mass of bullet = 8.73 g = 0.00873 kg

m₂ = mass of first block = 1201 g = 1.201 kg

m₃ = mass of second block = 1606 g = 1.606 kg

u₁ = initial speed of bullet = 345 m/s

u₂ = initial speed of first block = 0 m/s

u₃ = initial speed of second block = 0 m/s

v₁ = final speed of bullet = v₃ (since the bullet is embedded in second block)

v₂ = final speed of first block = 0.714 m/s

v₃ = final speed of second block = ?

Therefore,

`(0.00873\ kg)(345\ m/s)+(1.201\ kg)(0\ m/s)+(1.606\ kg)(0\ m/s)=(0.00873\ kg)(v_(3))+(1.201\ kg)(0.714\ m/s)+(1.606\ kg)(v_(3))`

`3.0118\ kg.m/s - 0.8575\ kg.m/s = (1.6147\ kg)(v_(3))\\\\v_(3) = (2.1543\ kg.m/s)/(1.6147\ kg) \\`

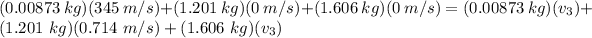
v₃ = 1.334 m/s