Question

In a filling line at A & C Foods, Ltd., the mean fill volume for rice bubbles is 475 grams and the standard deviation is 10 grams. The design specifications are [450, 495] grams. Any output outside of design specifications is treated as non-conforming. (1) Calculate the dpmo of the process (by calculating the area of non-conformance). Please type your answer in integers.

Answer 1

The dpmo of the process is of 29000

Explanation:

Dpmo of a process:

The dpmo of a process is the number of defects per million opportunities.

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

In this question:

First, using the normal distribution, we calculate the proportion of defective bubbles. Then, using this proportion, we calculate the dpmo.

Mean fill volume for rice bubbles is 475 grams and the standard deviation is 10 grams.

This means that
`\mu = 475, \sigma = 10`

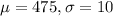
The design specifications are [450, 495] grams. Any output outside of design specifications is treated as non-conforming.

Below 450 and Above 495 are non-conforming.

Below 450:

The proportion is the pvalue of Z when X = 450. So

`Z = (X - \mu)/(\sigma)`

`Z = (450 - 475)/(10)`

`Z = -2.5`

`Z = -2.5` has a pvalue of 0.0062

Above 495:

The proportion is 1 subtracted by the pvalue of Z when X = 495. So

`Z = (X - \mu)/(\sigma)`

`Z = (495 - 475)/(10)`

`Z = 2`

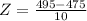
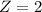
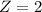`Z = 2` has a pvalue of 0.9772

1 - 0.9772 = 0.0228

The proportion of defectives is 0.0228 + 0.0062 = 0.0290

Dpmo:

Number of defects per million, that is, the proportion multiplied by 1000000.

1000000*0.0290 = 29000

The dpmo of the process is of 29000