Answer:
a. The probability that the percentage will be between 62% and 67% is 0.378348
b. For the central 90% the lack of trust in the financial industry is between 55.282% and 70.92%
c. For the probability within the central 95%, the lack of trust in the financial industry is between 56.77% and 56.77%%
d. Increasing the sample size increases the sensitivity and narrows the ranges and values
Explanation:
a. The percentage of the CFA members that indicated that lack of ethical culture within financial firms has contributed the most to the lack of trust in the financial industry, p = 63%
The test statistic is given as follows;
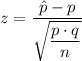
p = 63% = 0.63
q = 1 - p = 0.37
a. When
 = 62%, we get;
= 62%, we get;
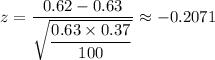
From the z-table the p-value p(z <-0.2071) = 0.42074, from the calculator, we get the more accurate value as p = 0.4179563
When
 = 67%, we get;
= 67%, we get;
(0.67 - 0.63)/((0.63*0.37)/100)^(0.5)
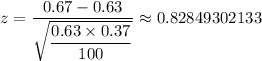
From the z-table the p-value p(z < 0.8) = 0.79673, from the calculator, we get the more accurate value as p(z < 0.828493) = 0.7963043
Therefore, using the calculator values, the probability that the percentage will be between 62% and 67% = 0.7963043 - 0.4179563 = 0.378348
The probability that the percentage will be between 62% and 67% = 0.378348
b. For the central 90% symmetrical limit, we get;
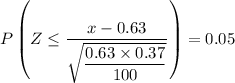
Therefore;
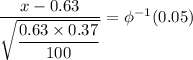
z = -1.64
Therefore;
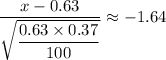
x = -1.64×√(0.63*0.37/100) + 0.63 ≈ 0.55282, which is 55.282%
Similarly, we get;
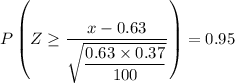
Therefore;
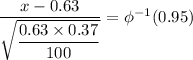
z = 1.64
Therefore;
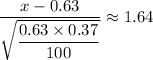
x = 1.64×√(0.63*0.37/100) + 0.63 ≈ 0.7092, which is 70.92%
Therefore, the central 90% is between 70.92% and 55.282%
Therefore, the lack of trust in the financial industry is between 55.282% and 70.92%
c. Given that the probability is 95%, we get
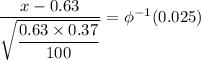
Therefore;

x = -0.67×√(0.63*0.37/100) + 0.63 ≈ 0.5977 = 56.77%
Similarly, we have;
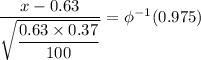
Therefore;
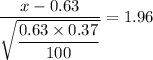
x = 1.96×√(0.63*0.37/100) + 0.63 ≈ 0.72463 =%
Therefore, at a probability of 95%, the lack of trust in the financial industry is between 56.77% and 56.77%%
d. Increasing the sample size increases the sensitivity and narrows the ranges and values such that we get;
For a) z = 0.62-0.63×√(0.63*0.37/400) ≈ 0.605
P ≈ 0.72907
0.67-0.63×√(0.63*0.37/400) ≈ 0.655
P ≈ 0.74527 - 0.72907 = 0.0162 = 1.62%
For b)
The p-value = 0.74527 -
-1.64×√(0.63*0.37/400) + 0.63 ≈ 0.5904 ≈ 59.04%
1.64×√(0.63*0.37/400) + 0.63 ≈ 0.7 = 70%
For c)
x = -0.67×√(0.63*0.37/400) + 0.63 ≈ 0.61383= 61.83%
x = 1.96×√(0.63*0.37/400) + 0.63 ≈ 67.73=%