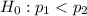Complete Question:
State whether each set of hypothesis is valid for a statistical test and briefly explain why ?


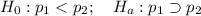
Answer:
 --- Valid
--- Valid
 --- Invalid
--- Invalid
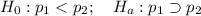 --- Invalid
--- Invalid
Explanation:
For a test of hypothesis to be valid, the null hypothesis has to contain some form of equality i.e.

So, the above will be used to test for validity in the given tests of hypotheses.

This is valid because the null hypothesis has an equality sign.
The null hypothesis is:


This is invalid because the null hypothesis does not have any equality sign. The null hypothesis is:
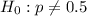
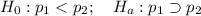
This is invalid because the null hypothesis does not have any equality sign. The null hypothesis is: