Question

Write an equation and solve.

A jar contained 10 marbles. The jar had five less than half as many as were on the table. How many marbles were on the table?

Answer 1

Let z represent the number of marbles on the table.

Note that:

• J = 10
• J = z/2 - 5

Thus, we can say that:

• J = 10 = z/2 - 5

Adding 5 to both sides:

• 5 + 10 = z/2 - 5 + 5
• => 10 + 5 = z/2

Simplifying the LHS:

• => 15 = z/2

Cross multiplication:

• => 15 x 2 = z
• => 30 = z

We can conclude that:

There were 30 marbles on the table.

Answer 2

30 marbles

Explanation:

Let,

No. of marbles on the table be = x

So,

No. of marbles in the jar =
`(x)/(2) - 5`

We know that,

No. of marbles in the jar were 10

Therefore,

By the problem,

=>
`(x)/(2) - 5` = 10

• [On adding 5 on both sides]

=>
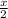`(x)/(2)` - 5 + 5 = 10 + 5

• [On simplification]

=>
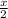`(x)/(2)` = 15

• [On multiplying both sides with 2]

=>
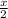`(x)/(2)` × 2 = 15 × 2

• [On simplification]

=> x = 30

Hence,

Required no. of marbles on the table were 30. (Ans)