Question

A point on a wheel moves at 32π/9 radians per minute. How many seconds are required for the point to complete 7 revolutions?

Answer 1

If you need to round up to the nearest tenth for this question, you'd put 236.3
:))

Answer 2

The number of seconds required to complete 7 revolutions is 236.28 s.

Explanation:

Given;

speed of the point on the wheel, ω = 32π/9 rad/min

number of revolutions made by the point, θ = 7 rev

The time taken for the point to make 7 revolutions is calculated as follows;

1 rev = 2π rad

`time (t) = (\theta )/(\omega) = \theta \ * (1)/(\omega) \\\\t = (7 \ rev \ * (2 \pi \ rad)/(1 \ rev) ) \ * ((1)/(32 \pi/9 \ (rad)/(\min) ) )\\\\t = (7 * 2\pi \ \ rad) * ((9)/(32 \pi )(\min)/(rad)) \\\\t = 14 \pi \ (rad) \ * \ (9)/(32 \pi)\ ((\min)/(rad) )\\\\t = (14 * 9)/(32) \ \min\\\\t = 3.938 \ \min\\\\t = 3.938 \ (\min) * (60 \ s)/(1 \ \min) \\\\t = 236.28 \ s`

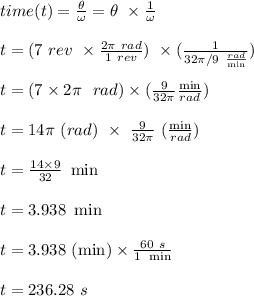
Therefor, the number of seconds required to complete 7 revolutions is 236.28 s.