Answer:
The largest possible volume of the box is 2000000 cubic meters.
Explanation:
The volume (
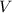 ), in cubic centimeters, and surface area (
), in cubic centimeters, and surface area (
 ), in square centimeters, of the box with a square base are described below:
), in square centimeters, of the box with a square base are described below:
 (1)
(1)
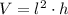 (2)
(2)
Where:
 - Side length of the base, in centimeters.
- Side length of the base, in centimeters.
 - Height of the box, in centimeters.
- Height of the box, in centimeters.
By (2), we clear
 within the formula:
within the formula:
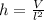
And we apply in (1) and simplify the resulting expression:
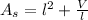
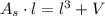
 (3)
(3)
Then, we find the first and second derivatives of this expression:
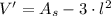 (4)
(4)
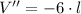 (5)
(5)
If
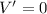 and
and
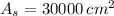 , then we find the critical value of the side length of the base is:
, then we find the critical value of the side length of the base is:
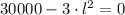
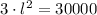
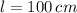
Then, we evaluate this result in the expression of the second derivative:
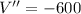
By Second Derivative Test, we conclude that critical value leads to an absolute maximum. The maximum possible volume of the box is:
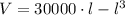
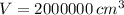
The largest possible volume of the box is 2000000 cubic meters.