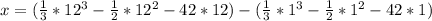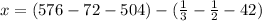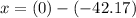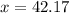Question

The velocity function, in feet per second, is given for a particle moving along a straight line. () = 2 − − 42, 1 ≤ ≤ 12

Answer 1

Question:

The velocity function, in feet per second, is given for a particle moving along a straight line.
`v(t) = t^2 - t - 42`
`1 \le t \le 12`

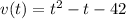
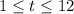
Find the displacement

Answer:

The displacement is 42.17ft

Explanation:

Given

`v(t) = t^2 - t - 42`
`1 \le t \le 12`

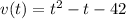
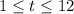
The displacement x, is calculated using:

`x = \int\limits^a_b {v(t)} \, dt`

`x = \int\limits^(12)_(1) {t^2 - t - 42} \, dt`

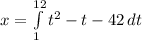
Integrate

`x = (1)/(3)t^3 - (1)/(2)t^2 - 42t|\limits^(12)_(1)`

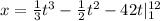
Substitute 12 and 1 for t respectively

`x = ((1)/(3)*12^3 - (1)/(2)*12^2 - 42*12) - ((1)/(3)*1^3 - (1)/(2)*1^2 - 42*1)`

`x = (576 - 72 - 504) - ((1)/(3) - (1)/(2) - 42)`

`x = (0) - (-42.17)`

`x = 42.17`