Answer:
θ '= 4975 rev
Step-by-step explanation:
For this exercise let's use the relationship between work and the change in kinetic energy
W = ΔK
the expression for work is
W = - τ Δθ
where the negative sign indicates that the torque is in the opposite direction to rotation
kinetic energy
K = ½ I w²
we substitute
- τ Δθ = 0 - ½ I w²
θ =
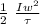
if we approach the rotor to a cylinder with an axis of rotation through its center
I = ½ m r²
we substitute
θ = ½ (½ m r²)
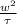
How the measurements are in the English system, the weight
W = m g
m = W / g
let's reduce to the english system
w = 3600 rev / min (2pi rad / 1rev) (1 min / 60s) = 376.99 rad / s
r = 9 in (1 ft / 12in) = 0.75 ft
let's calculate
m = 125/32 = 3.91 slug
θ = ¼ 3.91 0.75² 376.99² / 2.5
θ = 3.126 10⁴ rad
let's reduce to revolutions
θ’= 3.126 10⁴ rad (1rev / 2π rad)
θ’= 4974.9 rev
θ '= 4975 rev